LSTM是一种特殊的RNN，其引入状态量来保留历史信息，同时引入门的概念来更新状态量。

RNN：

LSTM：

原理

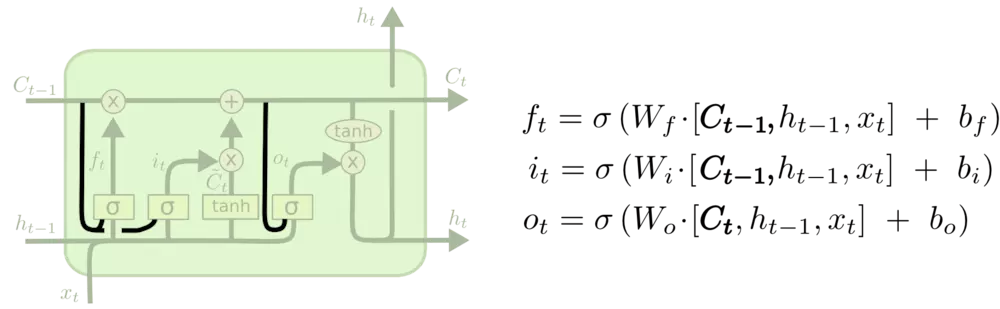
RNN网络中历史信息在每个RNN单元，都经过tanh/ReLu，信息在逐渐流失；而LSTM，采用信息更新的方式，更容易将有用的信息传递下去，传得更远。也就是下图中C随序列传递的过程。

为了实现状态量C的旧状态删除、新状态更新、当前结果有用状态信息的提取，分别引入“遗忘门”、“输入门”、“输出门”三个结构。

门：使用前一个输出，结合当前输入，通过sigmod函数，得到输出值，在0~1之间，决定信息量各部分被遗忘/选择的程度。

遗忘门

其中ht−1h_{t-1}ht−1表示的是上一个cell的输出，xtx_txt表示的是当前细胞的输入。$\sigma$表示sigmod函数。

输入门

输入门挑选信息来更新状态量C。

输出门

输出门挑选更新后的状态量C。

LSTM变体GRU

其中， rt表示重置门，zt表示更新门。重置门决定是否将之前的状态忘记。(作用相当于合并了 LSTM 中的遗忘门和传入门）当rt趋于0的时候，前一个时刻的状态信息ht−1会被忘掉，隐藏状态h^t会被重置为当前输入的信息。更新门决定是否要将隐藏状态更新为新的状态h^t（作用相当于 LSTM 中的输出门） 。

和 LSTM 比较一下：

1) GRU 少一个门，同时少了细胞状态Ct。

2) 在 LSTM 中，通过遗忘门和传入门控制信息的保留和传入；GRU 则通过重置门来控制是否要保留原来隐藏状态的信息，但是不再限制当前信息的传入。

3) 在 LSTM 中，虽然得到了新的细胞状态 Ct，但是还不能直接输出，而是需要经过一个过滤的处理；同样，在 GRU 中, 虽然我们也得到了新的隐藏状态h^t， 但是还不能直接输出，而是通过更新门来控制最后的输出：ht=(1−zt)∗ht−1+zt∗h^t

LSTM变体FC-LSTM

更新公式：

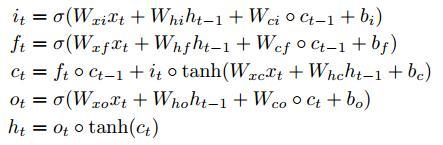
演示实验代码：

import torch
from torch import nn
import numpy as np
 
class Rnn(nn.Module):
    def __init__(self, INPUT_SIZE):
        super(Rnn, self).__init__()
 
        self.rnn = nn.LSTM(
            input_size=INPUT_SIZE,
            hidden_size=32,
            num_layers=2,
            batch_first=True
        )
 
        self.out = nn.Linear(32, 1)
 
    def forward(self, x, hc_state):
        # input(x): batch, seq_len, input_size = 1, 10, 2
        # output(r_out): batch, seq_len, hidden_size * num_directions = 1, 10, 32*1
        r_out, hc_state = self.rnn(x, hc_state)
 
        outs = []
        for time in range(r_out.size(1)):
            outs.append(self.out(r_out[:, time, :]))
        return torch.stack(outs, dim=1), hc_state
 
# 定义一些超参
TIME_STEP = 10
INPUT_SIZE = 2
LR = 0.02
# “看”数据
# plt.plot(steps, y_np, 'r-', label='target(cos)')
# plt.plot(steps, x_np, 'b-', label='input(sin)')
# plt.legend(loc='best')
# plt.show()
 
# 选择模型
model = Rnn(INPUT_SIZE)
print(model)
 
# 定义优化器和损失函数
loss_func = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=LR)
 
h_state = torch.autograd.Variable(torch.zeros(2,1,32)) # h0/c0: num_layers * num_directions, batch, hidden_size = 2*1, 1, 32
c_state = torch.autograd.Variable(torch.zeros(2,1,32)) # 第一次的时候，暂存为0
for step in range(300):
    start, end = step * np.pi, (step+1)*np.pi
 
    steps = np.linspace(start, end, TIME_STEP, dtype=np.float32)
    x_np = np.sin(steps)
    y_np = np.cos(steps)
 
    x = torch.from_numpy(x_np[np.newaxis, :, np.newaxis]) 
    y = torch.from_numpy(y_np[np.newaxis, :, np.newaxis])
 
    # 为了演示，重复x将输入数据特征扩展为两维
    prediction, (h_state, c_state) = model(torch.cat((x,x), 2), (h_state, c_state))
    h_state = h_state.data
    c_state = c_state.data
 
    loss = loss_func(prediction, y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
print("x:")
print(x)
print("y:")
print(y)
print("predict:")
print(prediction)