2.2 测量错误的方法

为了提高递归追踪的鲁棒性，我们使用了3条准则来滤除掉那些不可信追踪点。第一条准则是直接由等式2.5演变来的。由等式2.5可知，只有G可逆，才能求得d。从等式2.6可知，如果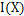在两个方向上的梯度存在，即G有两个特征值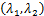，那么G可逆。我们采用Shi和Tomasi[45]提出的判决式，作为可信跟踪点的第一条准则。

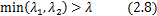
Kalal等提出了测量前后误差的方法，如图2.2所述。左图中的点1与右图中的对应点的跟踪是正确的。然而，由于闭塞的发生，点2最终追踪到一个错误的位置。这种测量错误的方法是基于点追踪必须可逆的思想提出的。点1可以追溯回起始点。然而，点2却追溯回一个不同于起始点的位置。采用欧氏距离来计算这种错误：

其中，

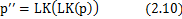
P’’表示对p运用两次Lucas and Kanade 光流法。

图2.2 前后误差测量法的思想是基于观察到某些点无法追溯回其原本位置提出的。 图源自[28]

引文[28]中的前后误差测量法是将该测量方法与另一种方法结合而得到的。另一种测量方法是计算p周围的图像块(patch)与追踪结果p’周围的图像块的相似度。P1、P2块的相似度可以由两幅图像中的P1块与P2块的归一化相关系数(NCC)得到。NCC的定义为：

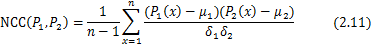
其中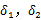，分别表示P1、P2的标准差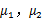；表示P1、P2的均值。由2.11可知，均匀亮度变化对归一化相关系数是没有影响的。